Set Operations (Discrete Math)

Set Operations

Frequently we need to combine sets to produce new sets. For instance, say we have a set of animals that live under the water and another set of animals that live on the ground. We could make a new set of animals that can live both, under water and on the ground. Or a set of animals that cannot live in water. There are a few ways of combining sets.

1. Intersections

Let's say that we have a set A = {1,2,3} and set B = {2,3,4}. Intersection of A and B is a new set - {2,3}. In other words, intersection is a set of objects that are present in multiple sets at the same time. In symbols, intersection is denoted by $\cap$ .
$A \cap B \thickspace is \thickspace \{e| \space e \in A \land e \in B \}$ Example,

{1,2,3} $\cap$ {2,3,4} = {2,3}

If two sets have no simultaneous objects, they are said to be disjoint sets.

Sometimes it is helpful to visualize sets to get the big picture. To do that we implement Venn Diagrams. Venn diagram - intersection

In the picture above, blue-purple area represents the intersection of A and B.

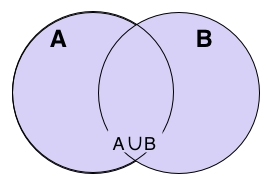
2. Union

Union is similar to intersection. With a small difference. When we want to represent the union of A and B, we take all the elements that appear in at least on of the sets. It does not include the duplicates. It is denoted by the symbol $\cup$ . In fancy symbols, we define it as the following: $A \cup B \thickspace is \thickspace \{e| \space e \in A \lor e \in B \}$

For instance,

{1,2,3,4} $\cup$ {3,5,6,7} = {1,2,3,4,5,6,7}

Venn diagram - Union

3. Symmetric Difference

Symmetric difference of A and B is a collection of objects that appear only in A or B. If an element is present in both sets, it cannot be a part of symmetric difference set. The special symbol to denote it is: $\oplus$ . $A \oplus B = \{ x| \space x \in A \oplus x \in B \}$

Example,

{1,2,3} $\oplus$ {2,3,4,5} = {1,4,5}

Since 2 and 3 appear in both sets above, they are not in the symmetric difference set. Venn diagram - Symmetric difference

4. Complement

The complement of B relative to A, written as $A - B$ (not $B - A$ ), is the set of elements that are present in set A and not in set B. $A - B = \{ x \mid x \in A \land x \notin B \}$ For example,

{1,2,3,4} $-$ {1,2,5,6} = {3,4}

Elements 3 and 4 exist in set one but not in set two. Hence, they are called the complement of B with respect to A. Sometimes they are called the difference of A and B.